Analyzing a Rope System: Theoretical vs. Actual Mechanical Advantage

Does a 3:1 rope system really give you a 3:1 mechanical advantage? Not exactly. When we talk about “3:1” advantage, we’re talking about a theoretical mechanical advantage. The actual mechanical advantage is what we experience in the field and accounts for friction caused by hardware and ropes coming in contact with an edge. It’s important for teams to know how to calculate an efficient system for each scenario. 

What Causes Friction? 

There are two primary causes of friction in a pulley. The first is the friction of the sheave rotating on the axle. By using a sealed ball bearing, friction can be significantly reduced. Sealed ball-bearing pulleys are permanently lubricated and sealed to keep out dirt and moisture, providing a long life. 

Friction in a pulley is also a result of the rope bending and unbending around the sheave as it goes into and out of the pulley. A softer, more pliable rope tends to be more efficient than a stiff rope. Tests have indicated that the difference in pulley efficiency can be as much as 15%, depending on the stiffness of the rope. 

Factors other than friction can decrease the effectiveness of a pulley system. One of the most common factors is not keeping the ropes parallel while pulling. As the haul line moves away from the M/A system, efficiency is lost.  

Using the T-Method to find the Actual Mechanical Advantage 

It’s important to calculate the actual mechanical advantage to help create an efficient rescue. If you are not familiar with the t-method or calculating theoretical mechanical advantage, please see our previous blog, Pulleys and Mechanical Advantage Systems. 

For this scenario, refer to the diagram below and assume each pulley is 85% efficient (resulting in 15% friction loss). Follow the steps below to determine actual mechanical advantage using the T-method: 

Start with one unit of tension applied to the input side of the mechanical advantage system, where the haul team grips the rope.

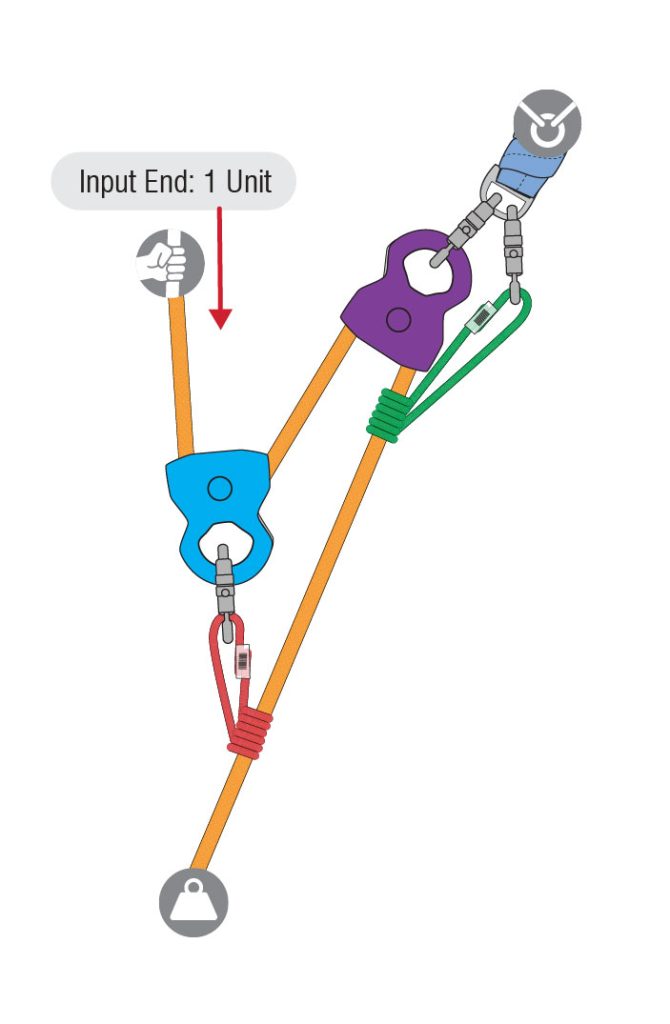
This one unit of tension enters the blue pulley, but due to friction loss of the blue pulley, only .85 comes out (1 unit – 15% friction loss = .85 units).

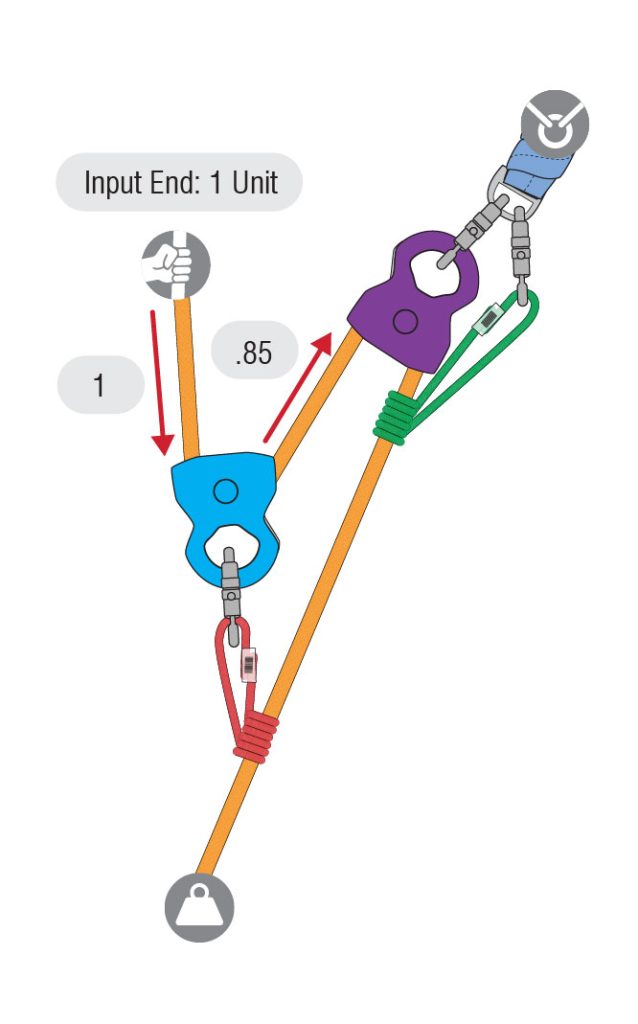
The addition of both units coming in and out of the blue pulley will produce a force of 1.85 units at the top of the blue pulley. The red Prusik hitch connects the blue pulley to the load line. Remember, the 1.85 units on the red Prusik hitch but follow the rope with .85 units.

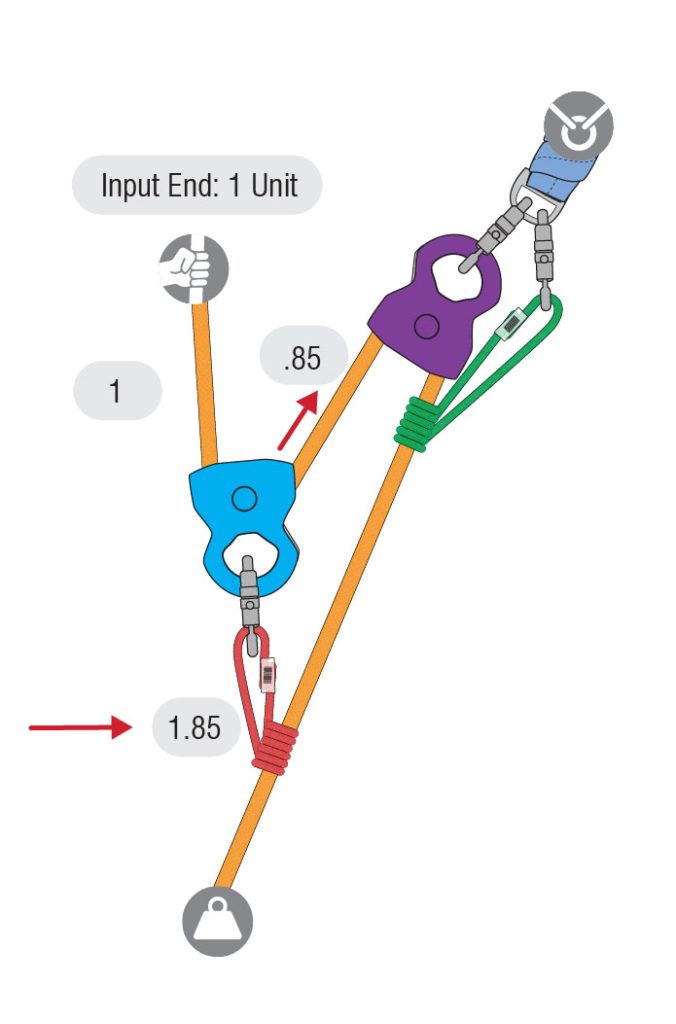
Continuing out of the blue pulley, the rope next enters and leaves a fixed purple pulley. Since this purple pulley does not move, the force is on the anchor and no units of force are added to the mechanical advantage. Therefore, .85 units of tension enter the purple pulley, and due to the 15% friction loss, .72 units exit the purple pulley. The green Prusik, used as a progress capture, is not loaded when hauling so it is not a part of the system at this time. While green Prusik adds some friction to the system, it is omitted for the simplicity of this example. 

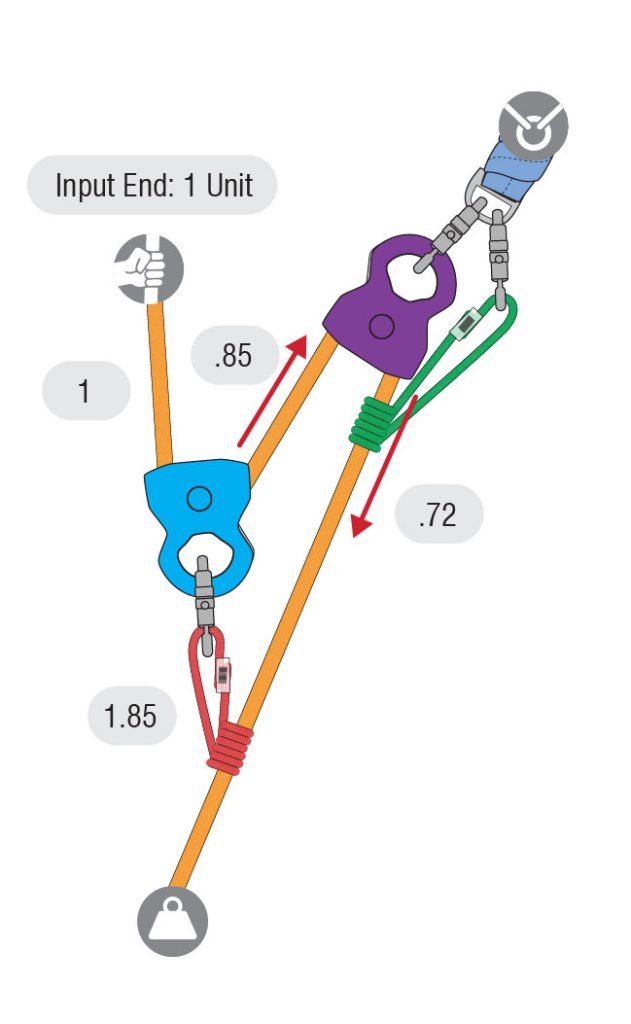
The .72 units of tension that exits the purple pulley then travels down the rope and meets up with the 1.85 units of tension at the red Prusik. Add these together to get 2.57 units of tension, making this a 2.57:1. We now know that this 3:1 theoretical simple mechanical advantage with 85% efficient pulleys has an actual mechanical advantage of 2.57:1. The diagrams below show the theoretical and actual mechanical advantage side by side. 

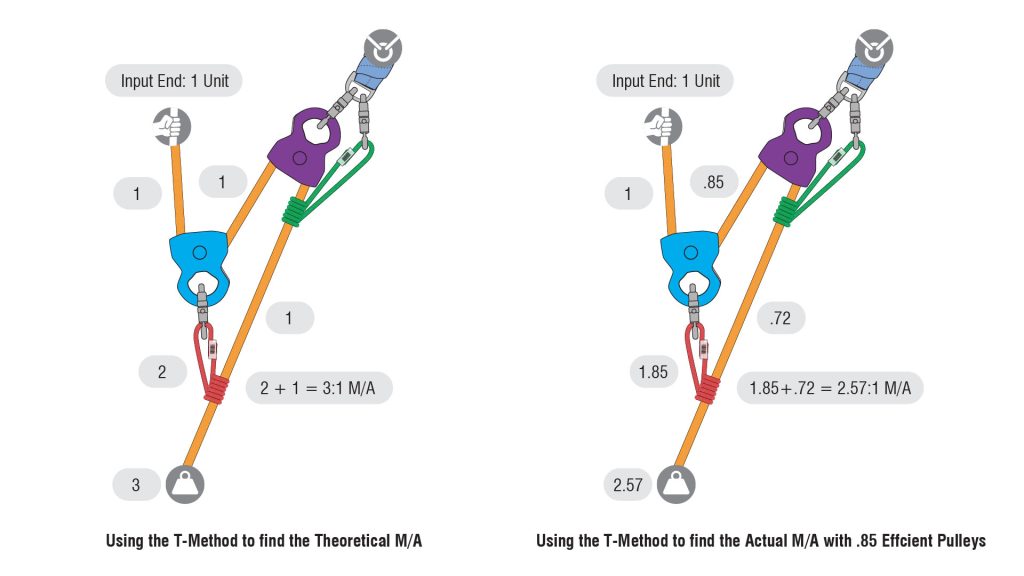
In the exercise below, determine the actual mechanical advantage of the system shown assuming all pulleys have an efficiency of 95%.  

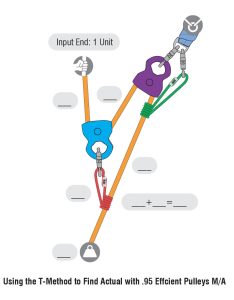
You should have come up with an actual mechanical advantage of 2.85:1.  

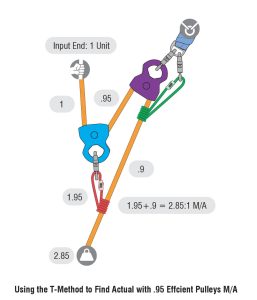
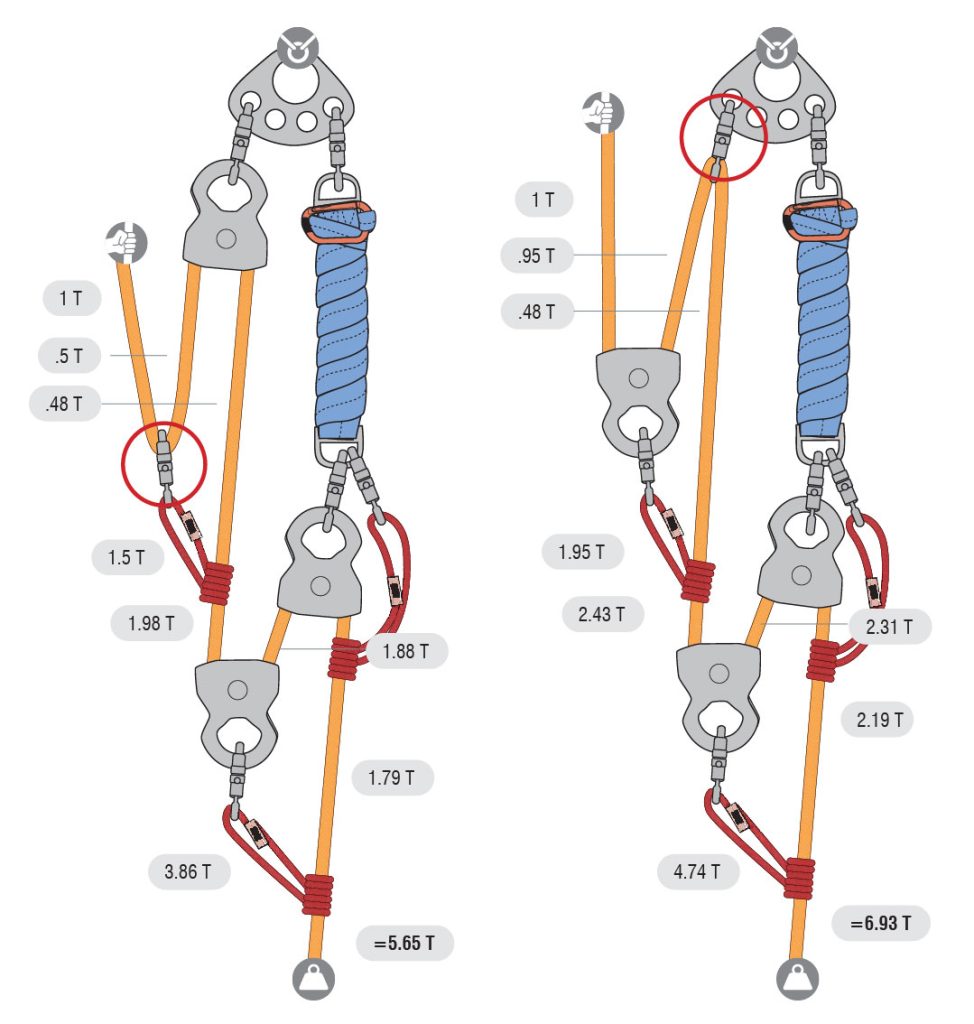
The effect of pulley efficiency on a mechanical advantage system is cumulative, meaning it increases with the number of pulleys (or sheaves) in the system. While a single change-of-direction pulley would reduce the output force by 5%, with four pulleys (or sheaves) in the system, the reduction of the output force approaches 20%. See images below for a t-system analysis of a 9:1 M/A system with pulleys that are 95% efficient and 85% efficient. 

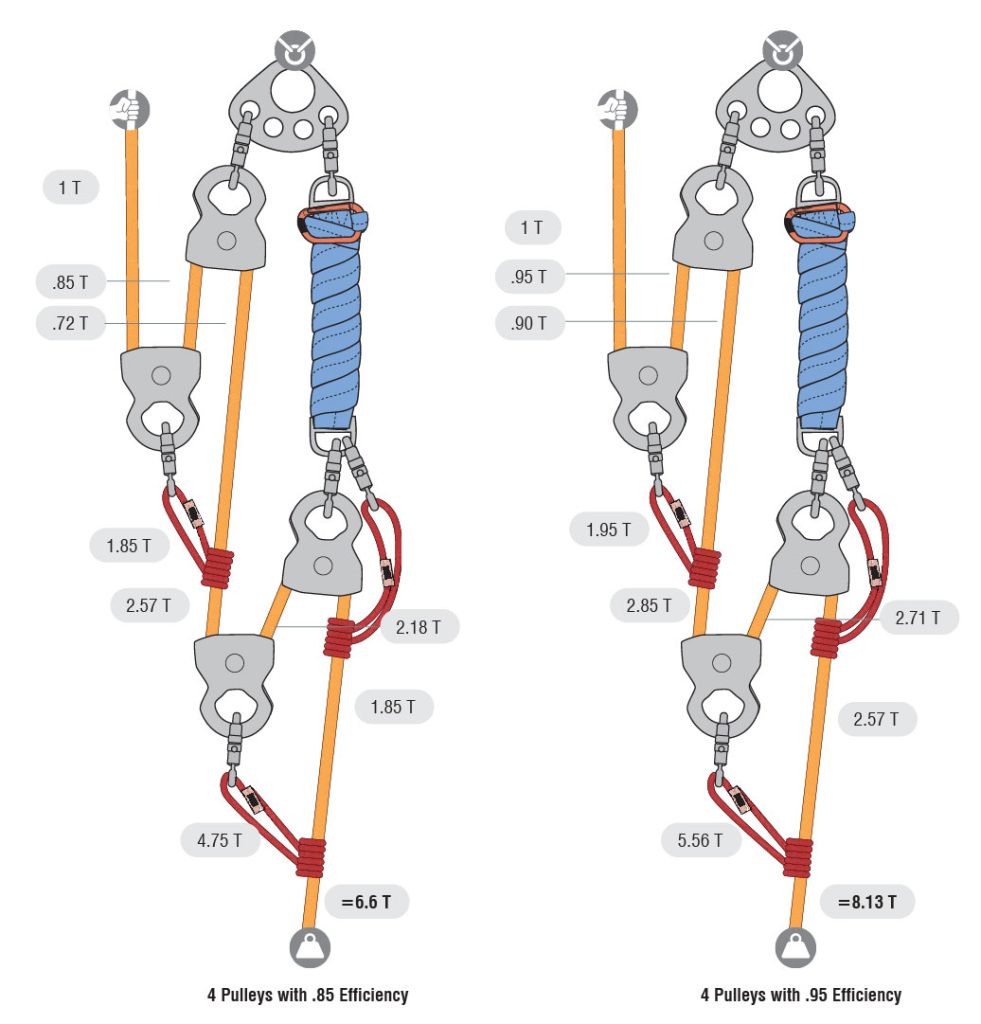
Suppose you do not have enough pulleys and need to run the rope through a carabiner to complete the system. The pulley efficiency between steel and aluminum carabiners varies slightly but it is usually around 50%. The diagrams below show using the T-method analysis on a 9:1 M/A to determine the best place to rig the carabiner for the maximum system output. 

Other Factors 

In this blog we have focused on friction caused by pulleys and carabiners. There are several other factors that can affect the actual mechanical advantage, such as bends in the rope over edges and wet nylon rope. 

To learn more about analyzing rope systems, check out the following resources: 

• Previous blog: Pulleys and Mechanical Advantage Systems. 
• CMC Field Guide App 
• CMC Rope Rescue Technician Manual and eBook 
• Find all of our educational resources with the CMC Tool Kit